You can perform matrix operations in Excel quickly, either directly or through the use of inbuilt matrix functions such as MMULT and TRANSPOSE. In this tutorial, we will learn how to perform matrix operations in Excel.
Also read: The Ultimate Guide to Using Sum Functions in Excel
Performing Matrix Operations in Excel
A matrix is is represented as A = [aij]. The entry in the ith row and jth column is denoted by the double subscript notation aij and bij. For example, a12 is an entry in the first row and second column.
Let’s get started with different matrix operations in Excel now.
1. Matrix addition in Excel
Matrix addition is the operation of adding two matrices in which each element of one matrix is added to the corresponding element of the other matrix to get their sum. Two matrices can be added together if and only if they have an equal number of rows and columns. If A = [aij] is an m*n matrix and B = [bij] is an m*n matrix, the reultant matrix A + B is an m*n matrix.
Let us consider two matrices of dimension 3*3 denoted by A and B for matrix addition:
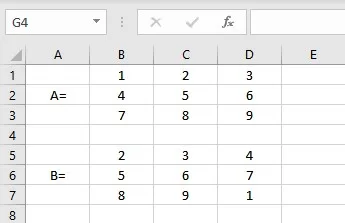
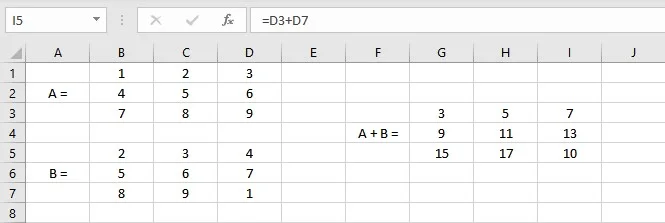
- Select the cell where you want to display the first element of the resultant matrix.
- Type =(B1: D3)+(B5: D7), where cells B1: D3 contain the elements of matrix A and B5: D7 contain the elements of matrix B.
- Press the Enter key if you have a current Microsoft 365 subscription else press CTRL+SHIFT+ENTER to display the resultant matrix.
2. Matrix subtraction in Excel
Matrix subtraction is the operation of subtracting one matrix from another in which each element of one matrix is subtracted from the corresponding element of the other matrix to get their difference. One matrix can be subtracted from another if and only if they have an equal number of rows and columns. If A = [aij] is an m*n matrix and B = [bij] is an m*n matrix, the reultant matrix A – B is an m*n matrix.
Let us consider two matrices of dimension 3*3 denoted by A and B for matrix subtraction:
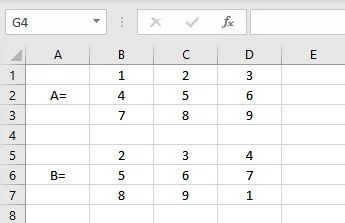
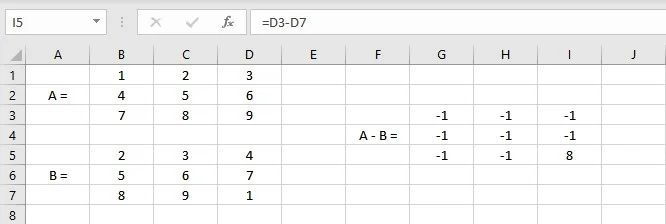
- Select the cell where you want to display the first element of the resultant matrix.
- Type =(B1: D3)-(B5: D7), where cells B1: D3 contain the elements of matrix A and B5: D7 contain the elements of matrix B.
- Press the Enter key if you have a current Microsoft 365 subscription else press CTRL+SHIFT+ENTER to display the resultant matrix.
3. Multiplication of a matrix by a scalar
In this operation, a scalar is multiplied by each element of the matrix to obtain the resultant matrix. If A = [aij] is an m*n matrix and λ is a scalar quantity, the resultant matrix λA = [ λ*aij] is an m*n matrix.
Let us consider a matrix of dimension 3*3 denoted by A for multiplication by a scalar:
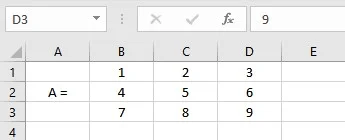
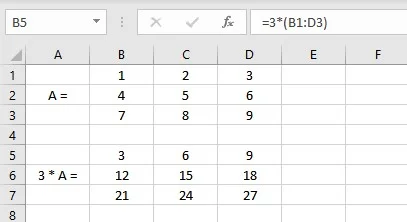
- Select the cell where you want to display the first element of the resultant matrix.
- Type =3*(B1: D3), where cells B1: D3 contain the elements of matrix A and 3 is a scalar.
- Press the Enter key if you have a current Microsoft 365 subscription else press CTRL+SHIFT+ENTER to display the resultant matrix.
4. Matrix multiplication
Matrix multiplication is a row-by-column multiplication which means the elements in the ith row of matrix A are multiplied with the corresponding elements in the jth column of matrix B and then added to obtain the elements of the product matrix. Two matrices can be multiplied if and only if the number of columns in the first matrix is the same as the number of rows in the second matrix. If A = [aij] is an m*n matrix and B = [bij] is an n*p matrix, the reultant matrix AB is an m*p matrix.
Let us consider two matrices of dimension 3*3 denoted by A and B for matrix multiplication:
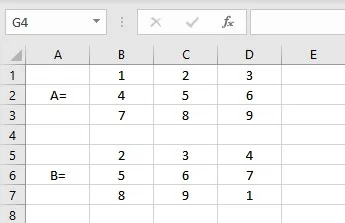
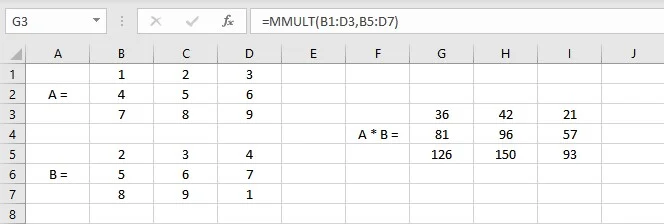
- Select the cell where you want to display the first element of the resultant matrix.
- Type =MMULT(B1: D3,B5: D7), where cells B1: D3 contain the elements of matrix A and B5: D7 contain the elements of matrix B.
- Press the Enter key if you have a current Microsoft 365 subscription else press CTRL+SHIFT+ENTER to display the resultant matrix.
Note: The MMULT function returns the #VALUE! error when the number of columns in the first matrix is not equal to the number of rows in the second matrix.
5. Transpose of a matrix
The transpose of a matrix is obtained by switching its rows with its columns. AT is used to denote the transpose of matrix A. If A = [aij] is an m*n matrix then AT = [aji] is an n*m matrix.
Let us consider a matrix of dimension 2*3 denoted by A for transposition:
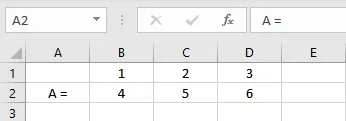
- Select the cell where you want to display the first element of the resultant matrix.
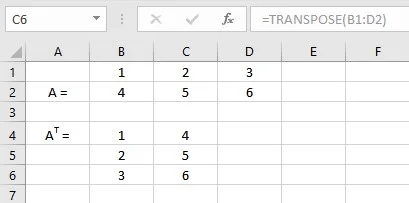
- Type =TRANSPOSE(B1: D2), where cells B1: D2 contain the elements of matrix A.
- Press the Enter key if you have a current Microsoft 365 subscription else press CTRL+SHIFT+ENTER to display the transpose of matrix A.
Conclusion
In this tutorial, we learned how to perform matrix operations such as addition, subtraction, multiplication by a scalar, multiplication of two matrices and to obtain transpose of a matrix.
