In this tutorial, we will learn 3 easy ways to calculate the square root of a number in Excel. It will be a very common calculation that you’ll perform very often if you work with large mathematical datasets of any kind. So let’s get started.
Different Ways to Calculate the Square Root in Excel
There are many different ways you can use to calculate square roots and here are some of the most common ones.
1. SQRT() function
Excel provides an inbuilt mathematical function SQRT to calculate the positive square root of a number.
Syntax: SQRT(n). Here n is the number or cell reference which contains the number for which you want the square root.
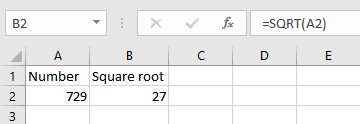
When the SQRT function is applied to a negative number, #NUM! error message is returned.
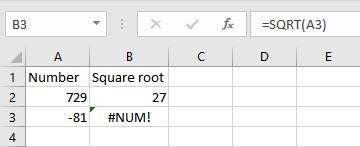
We can avoid the #NUM! error message, use the ABS function to find the absolute value of the number and then calculate the square root.
2. POWER() Function
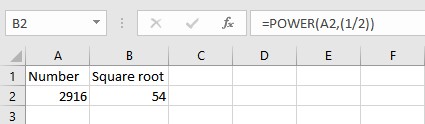
The POWER function returns the result of a number raised to a power. Syntax: POWER(n,power), where n is the base number or cell reference which contains the base number and power is the exponent to which the base number is raised. This function can be utilized to find the square root of a number by keeping power as 0.5 or (1/2).
3. Using the Caret ^ operator
We can use the caret operator ^ to raise a number to the power of half (1/2 or 0.5) and get the square root of the number.
Syntax: n^(1/2) or n^0.5, where n is the number or cell reference which contains the number for which you want the square root.
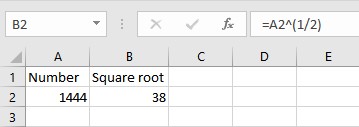
As you can see, we have the square root in the column B using the caret operator.
Conclusion
Excel provides a direct function SQRT to calculate the square root of a number. There are other simple methods to do the same which are discussed above. We hope you learned something new today!
