The value function in Excel is a type of text function that converts a text string or array that also represents a number into a numerical thing. This isn’t the final version of the text.
Consider the following scenario: we have a data set with a column that contains a currency amount. We can transform a currency figure with a currency signature into such a simple value using the Value function, which we can then conclude or use elsewhere.
Excel’s VALUE Formula:
The VALUE Function in Excel has the following formula:
=VALUE(Text)
The following arguments are used by the VALUE function:-
The VALUE function has only one argument, which is listed below. The text contained in quote marks or a reference to a cell that contains the text you would like to change is the Values (Required Argument / Text Value).
Steps For Using the VALUE Function
Here are the steps you should follow to use the VALUE function:
- Navigate to the Formulas tab.
- To access the Function drop-down menu, select Text.
- To open the function’s dialogue box, select VALUE from the list.
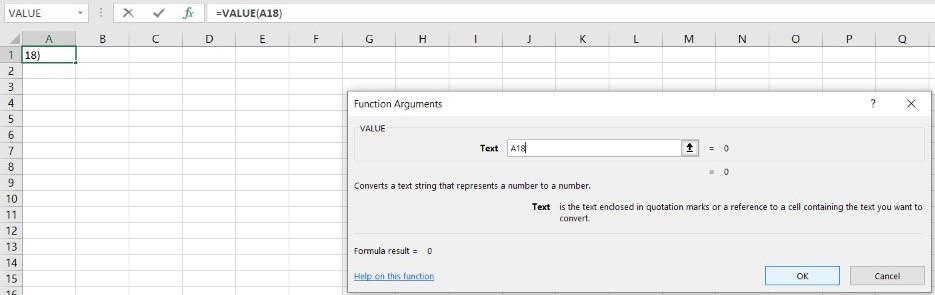
- Also, select the Insert function icon, then type and search the formula manually.
- In the screenshots below, we can see a new function window.
- In the open dialogue box, type the value.
- Then we must enter the information as indicated in the image.
- Wherever you want to convert the data type, but the Cell value or text value.
- Then select OK.
The following here is a shortcut for utilizing the Formula:
Tap on the cell wherever you wish the amount from the formula to appear, and then type in the formulas as shown below –
= Value (Cell Value / Text Value)
Using the Value Function in Excel
Excel’s Value Function is incredibly simple and straightforward to use. Let’s look at a few examples to see how the Value Function in Excel works.
Example 1 –
In the below image, we have a variety of data such as date, time, currency, numbers, numeric in-text value, and discount percentage.
We can see how to convert all of the data to a numeric value using the value function, and then perform any calculations on the result value using the formula below.
It returns the following result:
Example 2 –
As indicated in the screenshot below, there are certain details about calling agents in a call center. Agent name, initial login time, and last log-out time.
We may use the IF Function to verify which agent hasn’t completed the login period, and we can utilize the value function in this formula as we are given the timing criterion in text format.
We’re using the IF Function with a value function; the value function has been translated to time format and is given in text format in the criterion.
=IF (B2 >= VALUE ( “9:00 AM ” ), “Complete Login ”, “Short Login Duration ”)
With the aid of the value function and the IF Function, we can now get the result as shown below.
Example 3 –
As shown in the image below, there are the names of several fruits, their quantities, and we want to know the total number of fruits, thus we can use the value function with the left function to retrieve this information.
=VALUE (LEFT (A2, 2))
We can now achieve a result like this:
Things To Keep In Mind While Using VALUE In Excel
- If the data isn’t in an Excel-compatible format, it might be left as text.
- When this happens, certain functions like SUM or AVERAGE skip the values in certain cells, resulting in computation errors. The #VALUE error is returned.
- You may also identify the data type by its alignment; text data in a cell aligns to the left. On the right cell, the numbers and dates are aligned.
- The function turns text into a numeric value when it appears in a recognized format (a number in the text, a date or time format, currency, or a percentage).
- Excel translates text to numeric values when needed, thus the VALUE function isn’t required regularly.