In this tutorial, we’ll work with a few complex functions in Excel. Working with complex numbers is different from working with real numbers. This tutorial explores calculating values for complex numbers.
Complex Functions in Excel
Let’s get started with 9 complex functions that should know in excel if you’re working with scientific datasets.
1. IMABS function
The distance between the origin (0,0) and the point (x,y) in the complex plane is defined as the absolute value or the modulus of a complex number, x+yi. The formula for the absolute value of a complex number is given by:
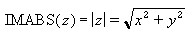
The IMABS function in Excel returns the absolute value of a complex number.
Syntax: IMABS(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the modulus is sought.
- Select the cell where you want to display the absolute value.
- Type =IMABS(, select the cell containing the complex number and finish the formula with ).
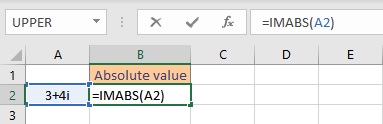
- Press the Enter key to display the result.
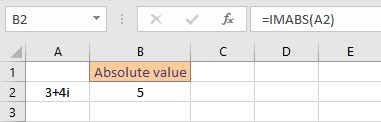
2. IMARGUMENT function
The angle made by the direction of the complex number from the real axis when it is represented on the complex plane is called the argument of a complex number. The argument of a complex number is given by:
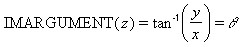
The IMARGUMENT function in Excel returns the argument of a complex number in radians.
Syntax: IMARGUMENT(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the argument is sought.
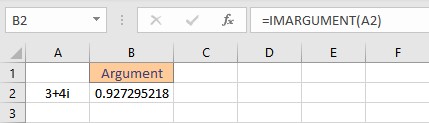
- Select the cell where you want to display the argument.
- Type =IMARGUMENT(, select the cell containing the complex number and finish the formula with ).
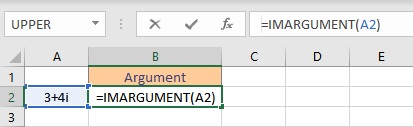
- Press the Enter key to display the result.
3. IMCONJUGATE function
The conjugate of a complex number is the reflection of that complex number on a complex plane about the real axis. The complex conjugate of x + iy is x – iy. The IMCONJUGATE function in Excel returns the conjugate of a complex number.
Syntax: IMCONJUGATE(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the conjugate is sought.
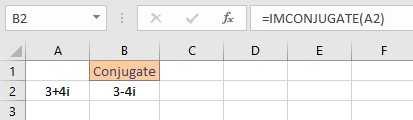
- Select the cell where you want to display the conjugate.
- Type =IMCONJUGATE(, select the cell containing the complex number and finish the formula with ).
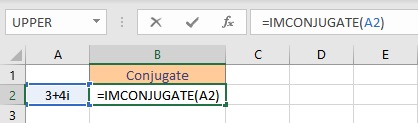
- Press the Enter key to display the result.
4. IMEXP function
The IMEXP function in Excel returns the exponential value of a complex number.
Syntax: IMEXP(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the exponential value is sought. The exponential of a complex number is given by:
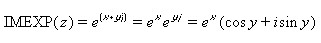
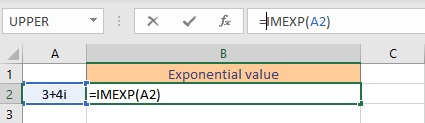
- Select the cell where you want to display the exponential value.
- Type =IMEXP(, select the cell containing the complex number and finish the formula with ).
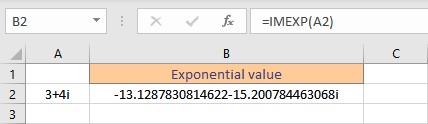
- Press the Enter key to display the result.
5. IMLN function
The IMLN function in Excel returns the natural logarithm of a complex number.
Syntax: IMLN(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the natural logarithm value is sought. The natural logarithm of a complex number is given by:
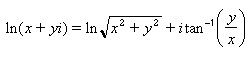
- Select the cell where you want to display the natural logarithm.
- Type =IMLN(, select the cell containing the complex number and finish the formula with ).
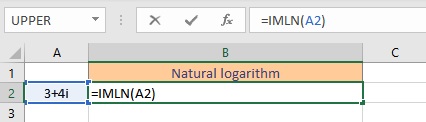
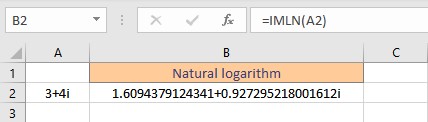
- Press the Enter key to display the result.
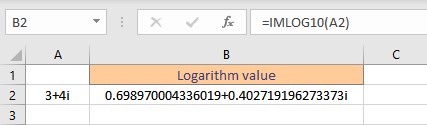
6. IMLOG10 function
The IMLOG10 function in Excel returns the base-10 logarithm of a complex number.
Syntax: IMLOG10(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the base-10 logarithm value is sought. The logarithm of a complex number is given by:
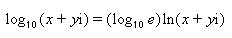
- Select the cell where you want to display the logarithm value.
- Type =IMLOG10(, select the cell containing the complex number and finish the formula with ).
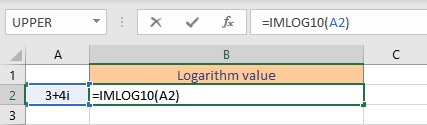
- Press the Enter key to display the result.
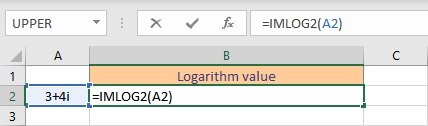
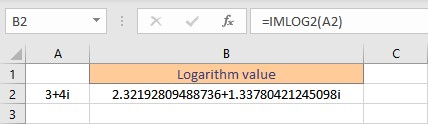
7. IMLOG2 function
The IMLOG2 function in Excel returns the base-2 logarithm of a complex number.
Syntax: IMLOG2(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the base-2 logarithm value is sought.
- Select the cell where you want to display the base-2 logarithm value.
- Type =IMLOG2(, select the cell containing the complex number and finish the formula with ).
- Press the Enter key to display the result.
8. IMPOWER function
The IMPOWER function in Excel returns the complex number raised to the desired power.
Syntax: IMPOWER(inumber,number),
where inumber is the complex number or the cell reference of the cell containing the complex number and number is the power to which you want to raise. The complex number raised to the desired power is given by:
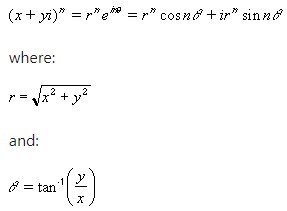
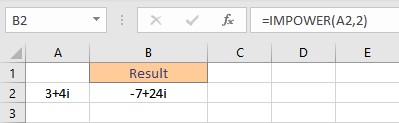
- Select the cell where you want to display the resultant value.
- Type =IMPOWER(A2,2) where A2 contains the complex number.
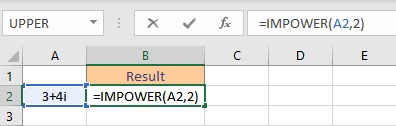
- Press the Enter key to display the result.
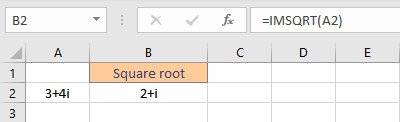
9. IMSQRT function
The IMSQRT function in Excel returns the square root of a complex number.
Syntax: IMSQRT(inumber),
where inumber is the complex number or the cell reference of the cell containing the complex number for which the square root is sought. The square root of a complex number is given by:
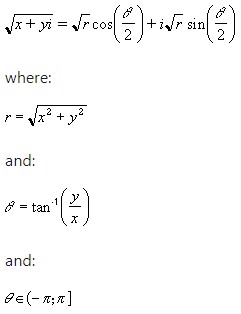
- Select the cell where you want to display the square root value.
- Type =IMSQRT(, select the cell containing the complex number and finish the formula with ).
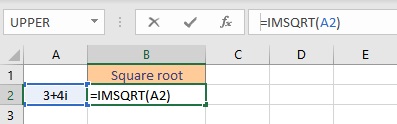
- Press the Enter key to display the result.
Conclusion
In this tutorial, we learned inbuilt functions in Excel to work with complex numbers.
References:
- IMABS function – Office Support (microsoft.com)
- IMARGUMENT function (microsoft.com)
- IMCONJUGATE function – Office Support (microsoft.com)
- IMEXP function (microsoft.com)
- IMLN function – Office Support (microsoft.com)
- IMLOG10 function (microsoft.com)
- IMLOG2 function (microsoft.com)
- IMPOWER function (microsoft.com)
- IMSQRT function – Office Support (microsoft.com)
